
Which is another setup having three parallel lines. If we start from type 2 and do not allow the other two types, there is essentially only one setup not already covered to consider: But with a line that only passes through the center the remaining two lines must covers $5$ points, so one of the lines must cover the $3$ points that are parallel to the initial $3$-line which again leads to a paralel $3$-lines contradiction. If we start from type 1 and do not allow type 2 and already know that type 3 must be ruled out and that no line parallel to the initial $3$-line is allowed, we see that this means that a line that passes the center point of the $9$ point pattern can pass no other point it the pattern as that would lead to one of the situations just mentioned. This makes it impossible to go through all points on any of these without visiting that line twice or reversing direction at some point. One way of seing why the above holds no solution is, that some of the lines are only intersected in ways having some of their points lying to both sides of the point of intersection. Which clearly does not hold a solution since the lines only intersect at one point so it takes far more than four linear moves to travel since you would have to return to this intersection time and again in any path traversing parts of all of these lines. When symmetries are considered, this gives essentially two setups to consider. So we have to have two lines passing through $2$ of the remaining $6$ points each that are not parallel nor orthogonal to the initial $3$-line of type 3. Also we can only have one line orthogonal to the $3$-line for otherwise we would again have parallel $3$-lines (in the orthogonal direction). This actually means that each of the remaining three lines has to cover exactly $2$ of the remaining $6$ points each. With the above we can rule out type 3 being a part of any solution: We cannot have any line parallel to the initial $3$-line by the above argument.

But three parallel lines are clearly impossible, since it takes two additional linear moves to visit and travel along all three, but we only have one line left! Ruling out type 3 So at least one line must cover more than one point which implies that the dashed grey line has to be added. When the two blue $3$-lines shown above have been placed we have to cover the remaining three points by two lines. For instance if we have the following situation: It is not possible to have a solution involving parallel $3$-lines. When identifying rotations and reflections we have exactly three distinct types of $3$-lines: Since four lines covering only $2$ points each can never cover $9$ points a solution has at least one $3$-line in it.
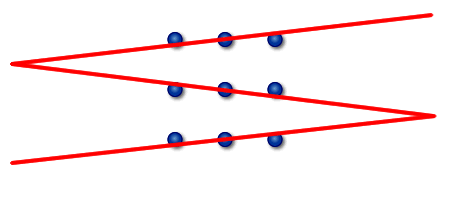
This question may require a more rigorous definition of "same picture" but I'm unable to think of a better way of describing it.įorget to begin with that we have to find a path, but simply try covering the $9$ points by four infinte straight lines.Ĭall a line covering $n$ points an $n$-line. How many solutions are there and how would you prove (other than through brute force) that the puzzle has only $K$ solution(s)? Treat solutions which are rotations or reflections of each other or solutions which generate the same "picture" despite their exact path as equivalent solutions. My initial thought is that, if the first solution is indeed the unique solution, then the Wikipedia article may be counting all the rotations, reflections, and alternate paths as different solutions to the puzzle because I can't think of another solution. Is just a $90\,^$ with the first two elements reversed and moved to the end of the path] In my cursory exploration of the puzzle, all the solutions I have found are either some rotation of the above solution or the same solution with a different starting point. In the Wikipedia page linked above, the solution is labeled as "One of many solutions to the puzzle." However, this page claims it's the unique solution to the puzzle. A solution is displayed below (spoiler alert): The aim of the Nine Dots Puzzle is to draw a path connecting 9 dots arranged in a $3\times 3$ grid using 4 continuous straight lines, never lifting the pen/pencil from the piece of paper.


 0 kommentar(er)
0 kommentar(er)
